10.6 Çok Boyutlu Diziler
10.6 Çok Boyutlu Diziler
Bir dizi aşağıdaki gibi bildirildiğinde bir boyutlu (tek indisli) dizi olarak adlandırılır. Bu tip dizilere vektör denir.
|
1 |
float a[9]; |
Bir dizi birden çok boyuta sahip olabilir. Örneğin iki boyutlu b dizisi şöyle tanımlanabilir:
|
1 |
float b[9][4]; |
İki boyutlu diziler matris olarak adlandırılır. ilk boyuta satır, ikinci boyuta sütün denir. Yukarıda b matrisinin eleman sayısı 9×4=36 dır. Bu durumda, genel olarak bir dizi şöyle gösterilir:
Tablo 10.1: Dizlerin Bildirimi
| Dizi Çeşiti | Genel Bildirimi | Örnek |
| Tek boyutlu diziler (Vektörler) | tip dizi_adı[eleman_sayısı] | int veri[10]; |
| İki boyutlu diziler (Matrisler) | tip dizi_adı[satır_sayısı][sutun_sayısı] | float mat[5][4]; |
| Çok boyutlu diziler | tip dizi_adı[boyut_1][boyut_2]...[boyut_n]; | double x[2][4][2]; |
Çok boyutlu diziler tek boyuta indir generek bellekte tutulurlar. Tek indisli dizilerde olduğu gibi, çok indisli dizilere de başlangıç değeri vermek mümkün. Örneğin 3 satır ve 4 sütünlu (3×4=12 elemanlı) bir x matrisinin elemanları şöyle tanımlanabilir:
|
1 |
int x[3][4] = {11,34,42,60, 72,99,10,50, 80,66,21,38}; |
yada
|
1 2 3 |
int x[3][4] = {11,34,42,60, /* 1. satır elemanları */ 72,99,10,50, /* 2. satır elemanları */ 80,66,21,38}; /* 3. satır elemanları */ |
Bu matris ekrana matris formunda yazılmak istendiğinde:
|
1 2 3 4 5 6 7 |
for(i=0; i<3; i++) { for(j=0; j<4; j++) printf("%4d",x[i][j]); printf("\n"); } |
çıktısı:
|
1 2 3 |
11 34 42 60 72 99 10 50 80 66 21 38 |
şeklinde olacaktır.
Program 10.8, iki matrisin toplamını başka bir matrise aktarır. Matris toplamı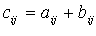 
formülü ile tanımlıdır. İnceleyiniz.
Program 10.8: İki matrisin toplamı
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
/* 09prg08.c: iki matrisin toplamı */ #include <stdio.h> #define SAT 2 #define SUT 3 int main() { int a[SAT][SUT] = {5, 3, 7, 0, 1, 2}; int b[SAT][SUT] = {1, 2, 3, 4, 5, 6}; int c[SAT][SUT]; int i, j; puts("A Matrisi:"); for(i=0; i<SAT; i++){ for(j=0; j<SUT; j++) printf("%4d",a[i][j]); printf("\n"); } puts("B Matrisi:"); for(i=0; i<SAT; i++){ for(j=0; j<SUT; j++) printf("%4d",b[i][j]); printf("\n"); } puts("\nC Matrisi:"); for(i=0; i<SAT; i++){ for(j=0; j<SUT; j++){ c[i][j] = a[i][j] + b[i][j]; printf("%4d",c[i][j]); } printf("\n"); } return 0; } |
ÇIKTI
|
1 2 3 4 5 6 7 8 9 10 |
A Matrisi: 5 3 7 0 1 2 B Matrisi: 1 2 3 4 5 6 C Matrisi: 6 5 10 4 6 8 |
Program 10.9, iki kare matrisin çarpımı başka bir matrise aktarır. Matris çarpımı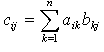 
formülü ile tanımlıdır.
Program 10.9: İki matrisin çarpımı
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
/* 10prg09.c: 3x3 boyutundaki iki kare matrisin çarpımı */ #include <stdio.h> #define N 3 int main() { int a[N][N], b[N][N], c[N][N]; int i,j,k,toplam; puts("A Matrisini girin:"); for(i=0; i<N; i++) for(j=0; j<N; j++) scanf("%d",&a[i][j]); puts("B Matrisini girin:"); for(i=0; i<N; i++) for(j=0; j<N; j++) scanf("%d",&b[i][j]); puts("\nC Matrisi:"); for(i=0; i<N; i++){ for(j=0; j<N; j++){ for(toplam=0, k=0; k<N; k++) toplam += a[i][k]*b[k][j]; c[i][j] = toplam; printf("%4d",c[i][j]); } printf("\n"); } return 0; } |
ÇIKTI
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
A Matrisini girin: 5 3 7 0 1 2 9 0 4 B Matrisini girin: 1 2 3 4 5 6 7 8 9 C Matrisi: 66 81 96 18 21 24 37 50 63 |
